Op Amps for Everyone Notes

Chapter 2 - Development of the Ideal Op Amp Equations

Ideal Op Amp

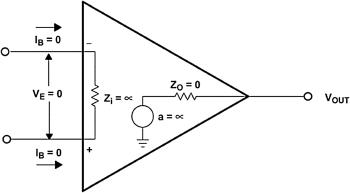
Parameter	Value
$I_{\text{IN}}$ - Input current	0
$V_{\text{OS}}$ - Input offset voltage	0
$Z_{\text{IN}}$ - Input impedance	$\infin$
$Z_{\text{OUT}}$ - Outage impedance	0
$a$ - Gain	$\infin$

From Wikipedia - Operational Amplifier:

• Infinite open-loop gain $G = v_{\text{out}} / v_{\text{in}}$
• Infinite input impedance $R_{\text{in}}$, and so zero input current
• Zero input offset voltage
• Infinite output voltage range
• Infinite bandwidth with zero phase shift and infinite slew rate
• Zero output impedance $R_{\text{out}}$, and so infinite output current range
• Zero noise
• Infinite common-mode rejection ratio (CMRR)
• Infinite power supply rejection ratio.

The Non-inverting Op Amp

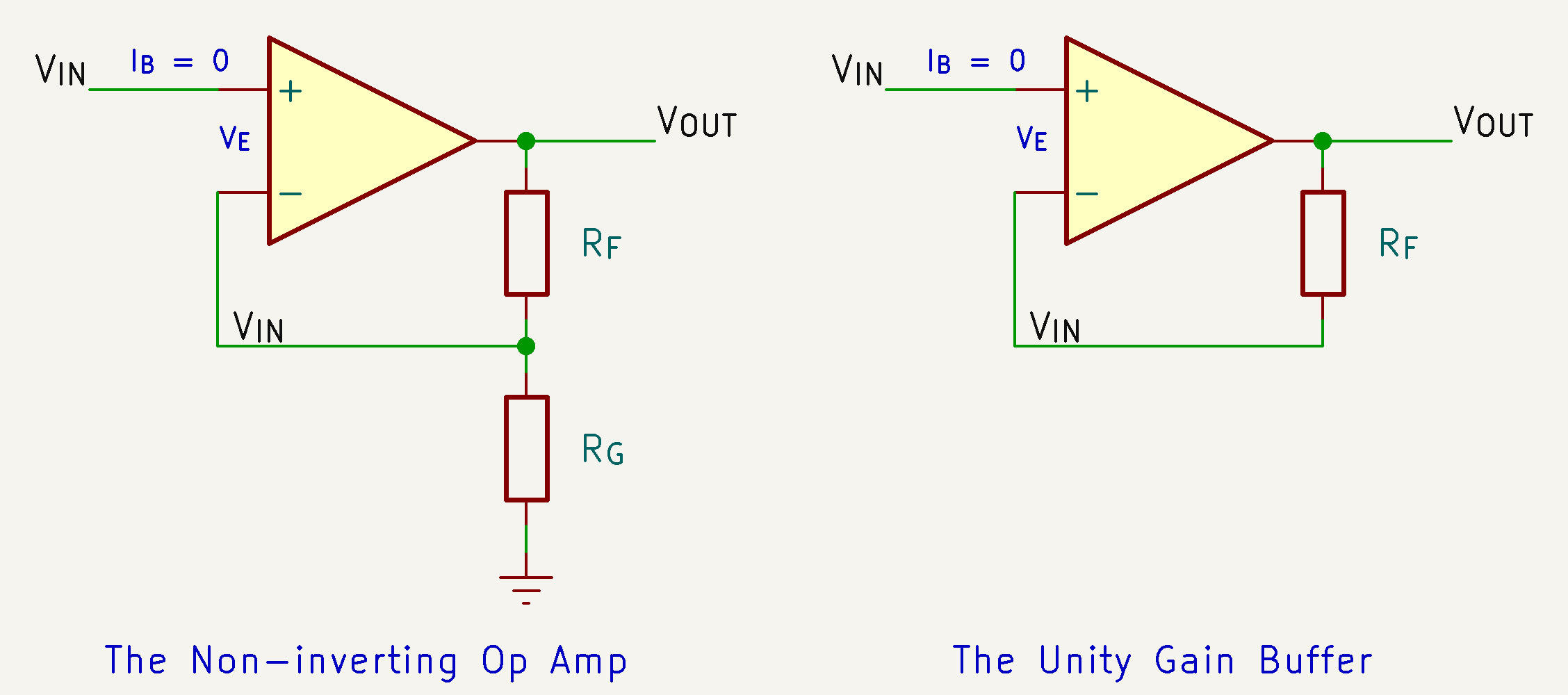
$$ \begin{align} V_{\text{OUT}} &= A_{\text{OL}}(V_{+} - V_{-}) \cr V_{-} &= \frac {R_{\text{G}}} {R_{\text{F}} + R_{\text{G}}} V_{\text{OUT}} = \beta V_{\text{OUT}} \end{align} $$

Substituting this into the gain equation, we obtain

$$ \begin{align} V_{\text{OUT}} &= A_{\text{OL}}(V_{\text{IN}} - \beta V_{\text{OUT}}) \end{align} $$

Solving for out $V_{{\text{OUT}}}$:

$$ \begin{align} V_{\text{OUT}} &= V_{\text{IN}} \left(\frac {1} {\beta + \displaystyle \frac {1} {A_{\text{OL}}}} \right) \end{align} $$

If $A_{\text{OL}}$ is vary large (100,000 or more), this simplifies to

$$ \begin{align} V_{\text{OUT}} \approx {\frac {V_{\text{IN}}}{\beta }} &= {\frac {V_{\text{IN}}}{\frac {R_{\text{G}}}{R_{\text{F}}+R_{\text{G}}}}}=V_{\text{IN}}\left(1+{\frac {R_{\text{F}}}{R_{\text{G}}}}\right) \cr \frac {V_{\text{OUT}}}{V_{\text{IN}}} &= \left(1+{\frac {R_{\text{F}}}{R_{\text{G}}}}\right). \end{align} $$

When $R_{\text{G}}$ becomes very large, $\displaystyle \frac {R_{\text{F}}}{R_{\text{G}}} \implies 0$, the circuit becomes a unity gain buffer.

$$ \frac {V_{\text{OUT}}}{V_{\text{IN}}} = 1 $$

• $R_{\text{G}} = \infin$ - Usually removed.
• $R_{\text{F}}$ is used to protect the inverting input from overvoltage.

The Inverting Op Amp

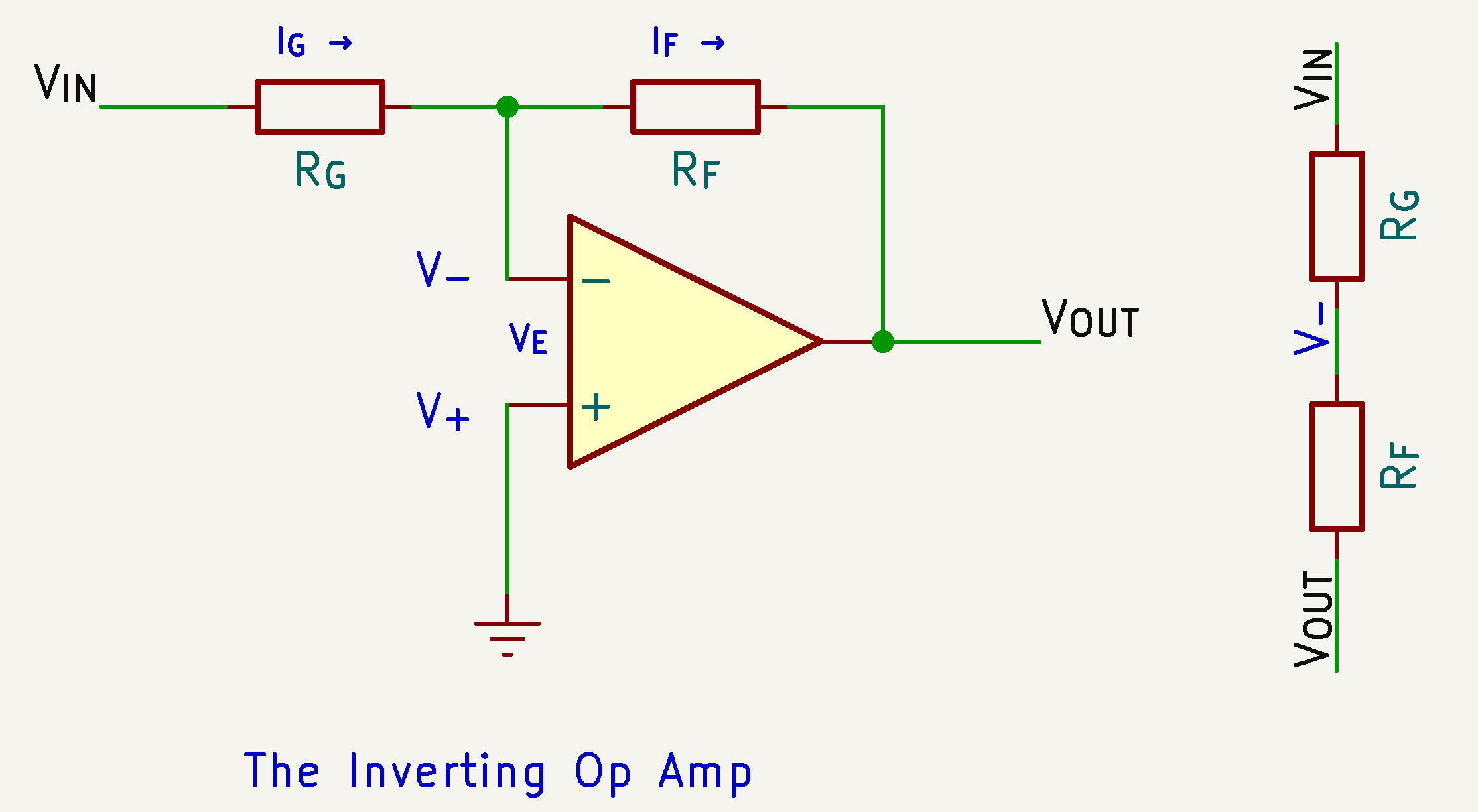
$$ \begin{align} V_{\text{OUT}} &= A_{\text{OL}}(V_{+} - V_{-}) \end{align} $$

$V_{-}$ is a function to $V_{\text{IN}}$ and $V_{\text{OUT}}$ due to $R_{\text{F}}$ and $R_{\text{G}}$.

$$ \begin{align} \frac{V_{\text{IN}}-V_{\text{OUT}}}{R_{\text{G}}+R_{\text{F}}} = \frac{V_{-}-V_{\text{OUT}}}{R_{\text{F}}} \cr V_{-} = \frac{R_{\text{G}}V_{\text{OUT}}+R_{\text{F}}V_{\text{IN}}}{R_{\text{G}}+R_{\text{F}}} \end{align} $$

Substituting this into the gain equation, we obtain

$$ \begin{align} V_{\text{OUT}} &= -A_{\text{OL}}\frac{R_{\text{G}}V_{\text{OUT}}+R_{\text{F}}V_{\text{IN}}}{R_{\text{G}}+R_{\text{F}}} \cr (R_{\text{G}}+R_{\text{F}})V_{\text{OUT}} &= -A_{\text{OL}}{R_{\text{G}}V_{\text{OUT}}-A_{\text{OL}}R_{\text{F}}V_{\text{IN}}} \cr V_{\text{OUT}} &= -V_{\text{IN}} \frac{A_{\text{OL}}R_{\text{F}}}{A_{\text{OL}}R_{\text{G}}+R_{\text{G}}+R_{\text{F}}} \end{align} $$

If $A_{\text{OL}}$ is vary large (100,000 or more), this simplifies to

$$ \begin{align} V_{\text{OUT}} &= -V_{\text{IN}} \frac{R_{\text{F}}}{R_{\text{G}}} \cr \frac{V_{\text{OUT}}}{V_{\text{IN}}} &= -\frac{R_{\text{F}}}{R_{\text{G}}} \end{align} $$

The Adder

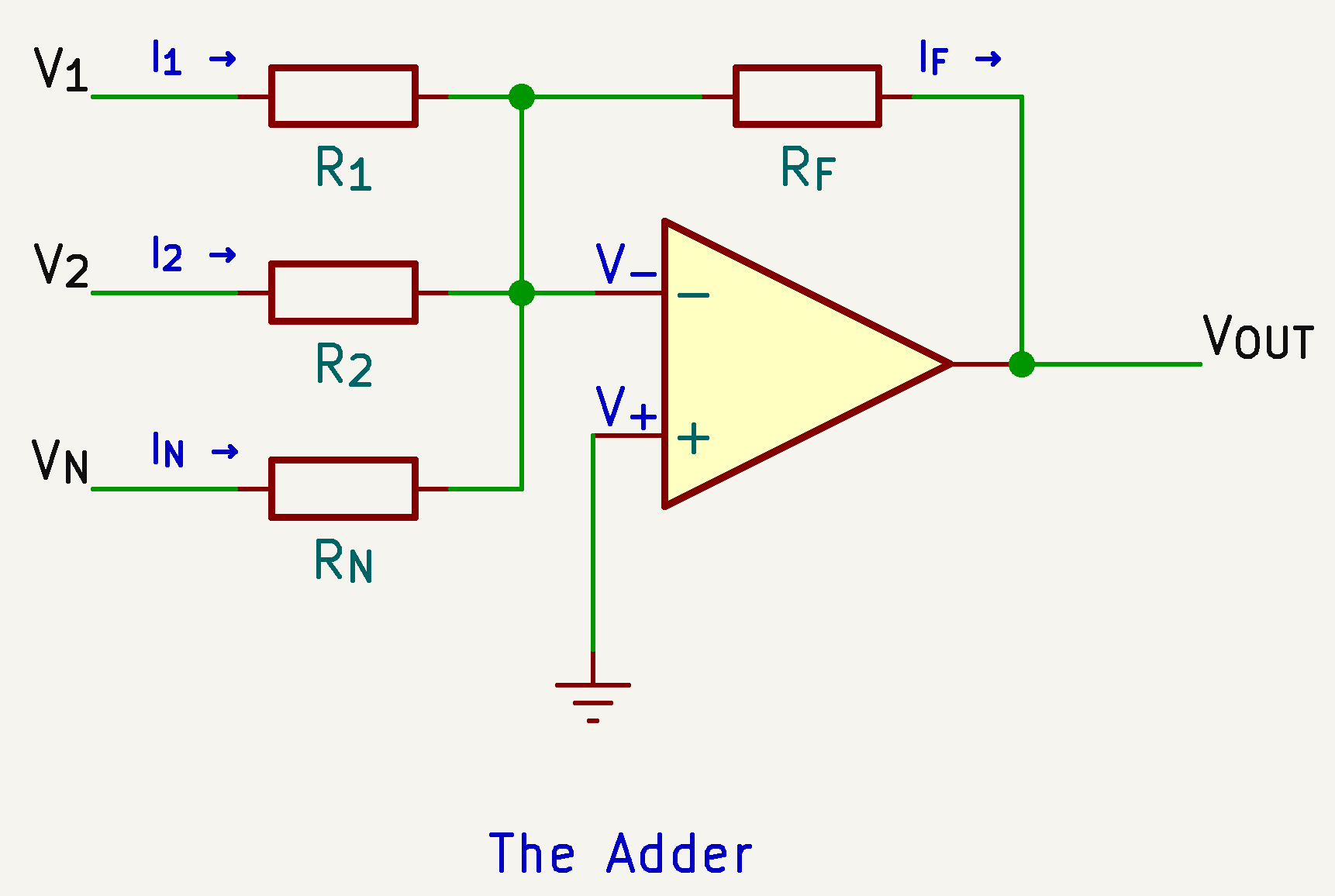
The non-inverting input is grounded, so the inverting input is virtually ground, there is no current flow through the inputs

$$ \begin{align} I_{\text{F}} &= I_{\text{1}} + I_{\text{2}} + I_{\text{N}} \cr \frac{0 - V_{\text{OUT}}}{R_{\text{F}}} &= \frac{V_{\text{1}}}{R_{\text{1}}} + \frac{V_{\text{2}}}{R_{\text{2}}} + \frac{V_{\text{N}}}{R_{\text{N}}} \cr V_{\text{OUT}} &= - \left(\frac{R_{\text{F}}}{R_{\text{1}}}V_{\text{1}} + \frac{R_{\text{F}}}{R_{\text{2}}}V_{\text{2}} + \frac{R_{\text{F}}}{R_{\text{N}}}V_{\text{N}} \right) \end{align} $$

The Differential Amplifier

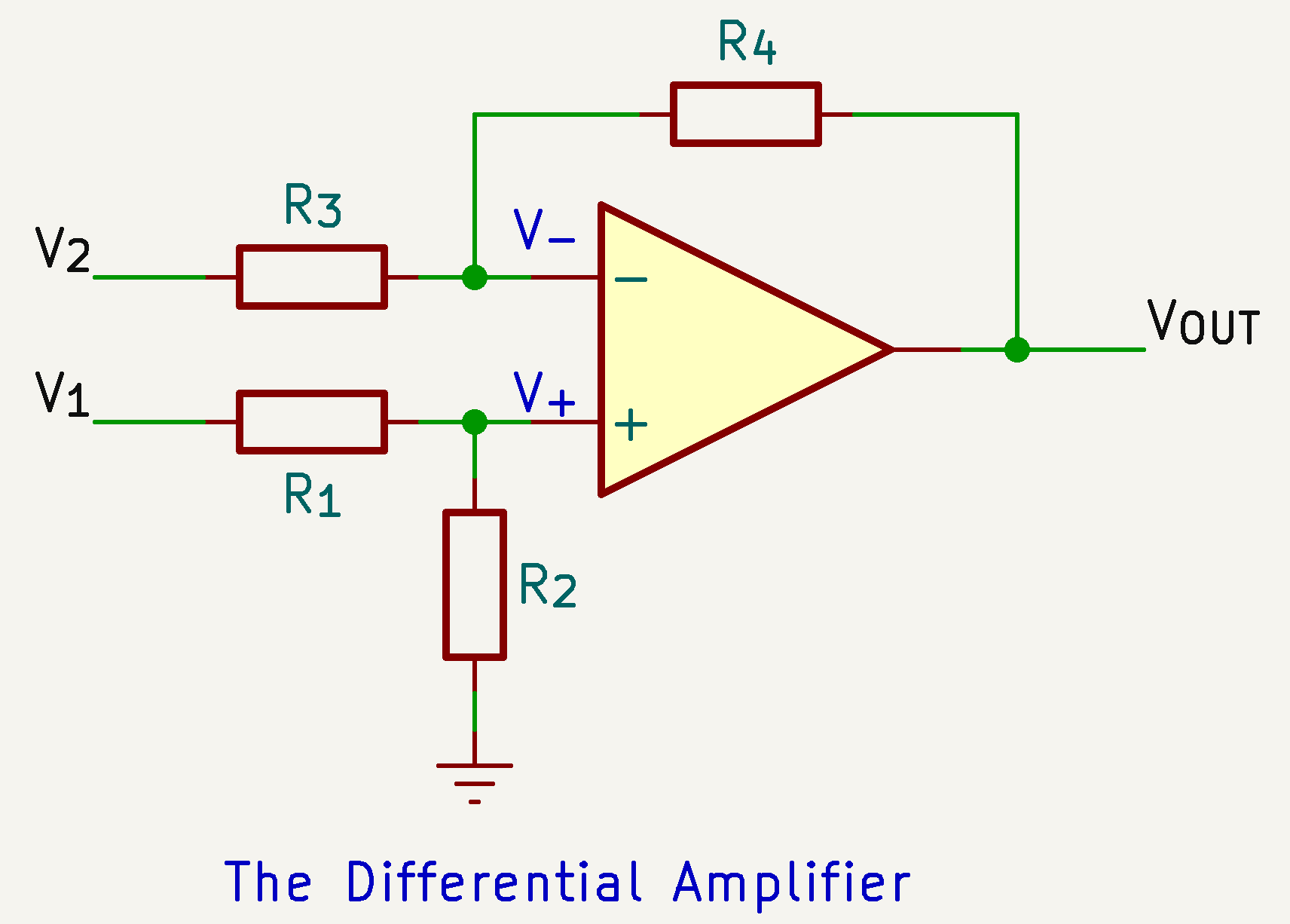
$$ \begin{align} V_{+} &= V_{\text{1}}\frac{R_{\text{2}}}{R_{\text{1}}+R_{\text{2}}} \cr \frac{V_{\text{OUT}}-V_{2}}{R_{\text{3}}+R_{\text{4}}} &= \frac{V_{-} - V_{\text{2}}}{R_{\text{3}}} \cr V_{\text{OUT}} &= V_{-}\frac{R_{\text{3}}+R_{\text{4}}}{R_{\text{3}}}- V_{\text{2}} \frac{R_{\text{4}}}{R_{\text{3}}} \cr \end{align} $$

Consider $V_{+} = V_{-}$, we have

$$ \begin{align} V_{\text{OUT}} &= V_{\text{1}}\frac{R_{\text{3}}+R_{\text{4}}}{R_{\text{3}}} \frac{R_{\text{2}}}{R_{\text{1}}+R_{\text{2}}} - V_{\text{2}}\frac{R_{\text{4}}}{R_{\text{3}}} \cr \end{align} $$

If the resisters $R_{\text{1}} = R_{\text{3}}$ and $R_{\text{2}} = R_{\text{4}}$, this simplifies to

$$ \begin{align} V_{\text{OUT}} &= (V_{\text{1}} - V_{\text{2}})\frac{R_{\text{2}}}{R_{\text{1}}} = (V_{\text{1}} - V_{\text{2}})\frac{R_{\text{4}}}{R_{\text{3}}} \end{align} $$